はじめに
音声の生成過程をソースとフィルタによってモデル化する手法として、ソースフィルタモデル[4]が知られています。 今回、このフィルタをARモデルを用いて実装し、ソースフィルタモデルによるシンプルなボイスチェンジャを作成しました。
やったこと
- ARモデルを用いてスペクトル包絡を推定
- そのスペクトル包絡を用いてボイスチェンジャを実装
ソースフィルタモデルによる音声合成
ソースフィルタモデルは、音声の生成仮定をソースとフィルタによってモデル化します。 ここで、ソースとは声帯による生成音を、フィルタとは声道による音響的な変化をそれぞれ表します。 この時、ソースとフィルタの関係を線形であると仮定すると、以下の様に表現することができます。
\[
Y\left(z\right) = H\left(z\right)X\left(z\right)
\]
上式において、\(Y\left(z\right)\)は音声信号を、\(X\left(s\right)\)はソースを、\(H\left(z\right)\)はフィルタをそれぞれ表します。 また、フィルタ\(H\left(z\right)\)はスペクトル包絡を、ソース\(X\left(z\right)\)は基本周波数成分をそれぞれ表現していると考えることができます。
ARモデルによるフィルタの実装
ソースフィルタモデルにおけるフィルタの実装方法には様々な手法ががあります。 ここでは、シンプルな手法であるARモデル[3]を用いました。 ARモデルは、以下の様に表現することができます。
\[
y\left(n\right) = \sum_{k=1}^{p}a_{k}y\left(n-k\right) + \epsilon\left(n\right)
\]
ここで、\(y\left(n\right)\)はフィルタの出力および観測信号を、\(a_{k}\)はAR係数を、\(\epsilon\left(n\right)\)はノイズをそれぞれ表します。 一般的に、AR係数の推定は誤差\(e\left(n\right)\)を最小化するように行われます。 このAR係数の推定には様々な手法があります。最も単純な方法は、以下の様にN個の関係式から最小二乗法を用いて推定する方法です。
\[\begin{align}
\mathbf{y}&=
\begin{pmatrix}
y\left(p\right) \\
y\left(p + 1\right) \\
\vdots \\
y\left(N - 1\right) \\
\end{pmatrix} \\
&= \begin{pmatrix}
y\left(p - 1\right) & \cdots & y\left(0\right) \\
\vdots & \ddots & \vdots \\
y\left(N - 2\right) & \cdots & y\left(N - 1 - p\right) \\
\end{pmatrix}
\begin{pmatrix}
a_{1} \\
\vdots \\
a_{p} \\
\end{pmatrix}\\
&= \mathbf{D} \mathbf{a} \\
\mathbf{a} &= \left(\mathbf{D}^{T}\mathbf{D}\right)^{-1}\mathbf{D}^{T}\mathbf{y}
\end{align}\]
しかしながら、この最小二乗法によって推定されたAR係数は必ずしも安定ではありません。 そのため、自己相関関数を用いてAR係数を推定する方法がよく用いられます。 自己相関法では、以下の様に定義する信号\(y'\left(n\right)\)を用いてAR係数の推定を行います。
\[\begin{align}
y'\left(n\right) = \left\{
\begin{array}{ll}
y\left(n\right) & \mathrm{if}\ n = 0, \dots , N - 1 \\
0 & \mathrm{others}
\end{array}
\right.
\end{align}\]
また、自己相関関数\(r\left(k\right)\)を以下の様に定義します。
\[\begin{align}
r\left(k\right) &= \sum_{n=-\infty}^{\infty}y'\left(n\right)y'\left(n + k\right)
\end{align}\]
すると、AR係数は以下の様に推定することができます。
\[\begin{align}
\mathbf{r}&=
\begin{pmatrix}
r\left(1\right) \\
r\left(2\right) \\
\vdots \\
r\left(p\right) \\
\end{pmatrix} \\
&= \begin{pmatrix}
r\left(0\right) & r\left(1\right) & \cdots & y\left(p - 1\right) \\
r\left(1\right) & r\left(0\right) & \cdots & y\left(p - 2\right) \\
\vdots & \vdots & \ddots & \vdots \\
y\left(p - 1\right) & r\left(p - 2\right) & \cdots & y\left(0\right) \\
\end{pmatrix}
\begin{pmatrix}
a_{1} \\
\vdots \\
a_{p} \\
\end{pmatrix}\\
&= \mathbf{R} \mathbf{a} \\
\mathbf{a} &= \mathbf{R}^{-1}\mathbf{r}
\end{align}\]
なお、上述の行列\(\mathbf{R}\)はテプリッツ行列[2]と呼ばれる特殊な形式となります。 今回は取り扱いませんが、テプリッツ行列の逆行列はレビンソン・ダービンのアルゴリズムを用いることで高速に計算することが可能です。
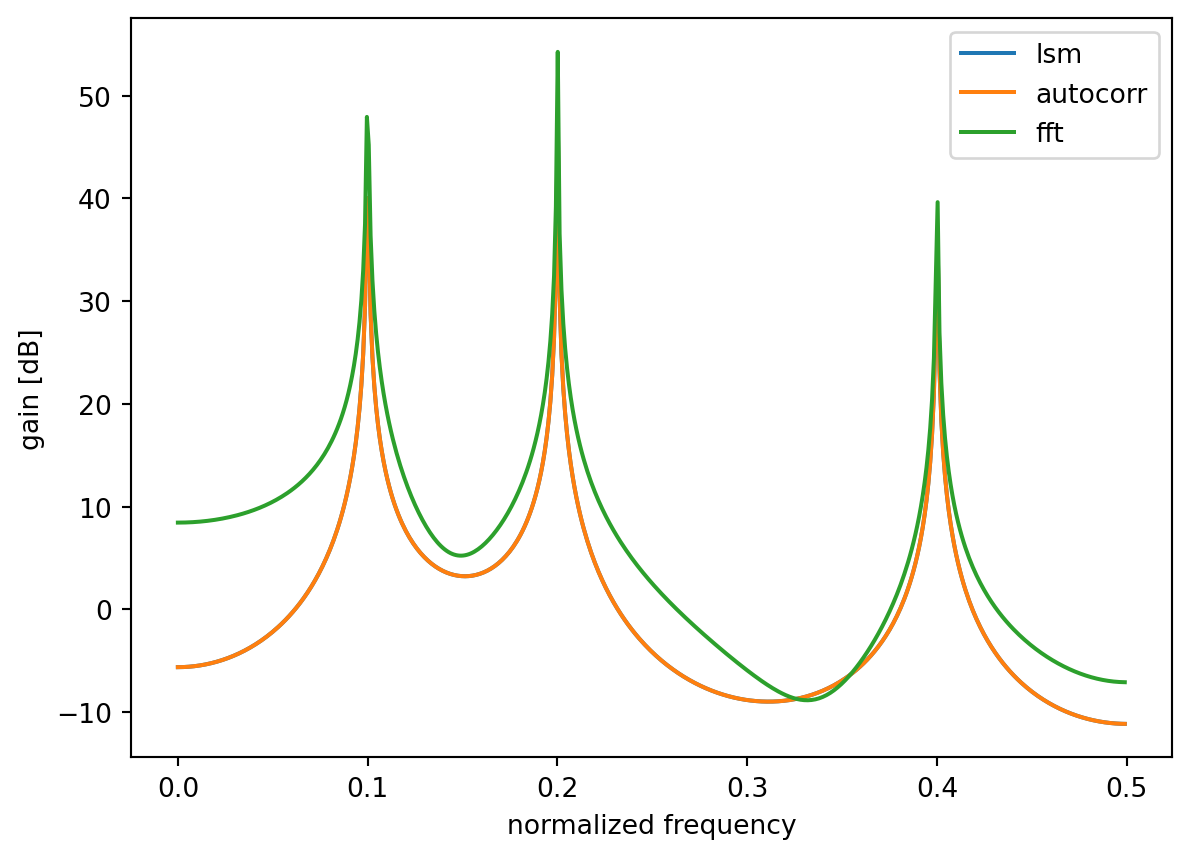
以下に、最小二乗法と自己相関法によるAR係数の推定を行うコードとその実行結果を示します。
import numpy as np
import numpy.typing as npt
from scipy import signal
import matplotlib.pyplot as plt
def calc_ar_coeff_by_lsm(y: npt.NDArray[np.float32], p: int) -> npt.NDArray[np.float32]:
stride = y.strides[0]
D = np.fliplr(np.lib.stride_tricks.as_strided(y, (len(x) - p, p), (stride, stride)))
Y = y[p:]
A = -np.linalg.solve(D.T @ D, D.T @ Y).astype(np.float32)
return np.concatenate([np.array([1]), A])
def calc_ar_coeff_by_autocorrelation(y: npt.NDArray[np.float32], p: int) -> npt.NDArray[np.float32]:
y = np.concatenate([np.zeros(p - 1, dtype=np.float32), y, np.zeros(p - 1, dtype=np.float32)])
Y = np.fliplr(np.lib.stride_tricks.sliding_window_view(y, p))
r = Y.T @ np.concatenate([y[p:], np.array([0])])
R = Y.T @ Y
A = -np.linalg.solve(R, r).astype(np.float32)
return np.concatenate([np.array([1]), A])
ns = 4096
t = np.linspace(0, 2 * np.pi, ns)
x = 0.8 * np.sin(0.1 * ns * t) + 0.5 * np.sin(0.2 * ns * t) + 0.3 * np.sin(0.4 * ns * t)
a_lsm = calc_ar_coeff_by_lsm(x, 6)
a_autocorr = calc_ar_coeff_by_autocorrelation(x, 6)
fig = plt.figure()
ax = fig.add_subplot(111)
w_lsm, h_lsm = signal.freqz(1, a_lsm)
ax.plot(w_lsm / (2 * np.pi), 20 * np.log10(np.abs(h_lsm)), label='lsm')
w_autocorr, h_autocorr = signal.freqz(1, a_lsm)
ax.plot(w_autocorr / (2 * np.pi), 20 * np.log10(np.abs(h_autocorr)), label='autocorr')
ax.plot(w_lsm / (2 * np.pi), 20 * np.log10(np.abs(np.fft.fft(x))[:2048:4]), label='fft')
ax.set_xlabel('normalized frequency')
ax.set_ylabel('gain [dB]')
ax.legend()
plt.show()
パルス列と白色雑音によるソースの実装
参考文献[4]によると、音声合成では有声音をパルス列で、無声音を白色雑音で表現すると良いとされているようです。 しかしながら、今回の目的はボイスチェンジャの実装であるため、これらの区別は行わずそれぞれを単一のソースとして扱います。
以下にパルス列と白色雑音を生成するコードを示します。
def gen_pulse(ns: int, f: float) -> npt.NDArray[np.float32]:
while True:
x = np.zeros(ns, dtype=np.float32)
interval = int(1.0 / f)
for i in range(0, ns, interval):
x[i] = 1.0
yield x
def gen_white_noise(ns: int) -> npt.NDArray[np.float32]:
while True:
yield np.random.normal(-1, 1, ns)
ボイスチェンジャの実装
フィルタとソースの実装が完了したので、それらを組み合わせてボイスチェンジャを実装します。 以下にコードを示します。
from datasets import load_dataset
from typing import Literal
common_voice = load_dataset("common_voice", "ja")
audio = common_voice["train"][0]["audio"]["array"]
sampling_rate = common_voice["train"][0]["audio"]["sampling_rate"]
def synth_voice(clip: npt.NDArray[np.float32], /, sampling_freq: float, source_freq: float = 0.00001, chunk_ms: float = 6, p: int = 64, source_type: Literal['pluse', 'noise'] = 'pluse') -> npt.NDArray[np.float32]:
chunk_size = int(sampling_rate * chunk_ms / 1000)
clip_length = (clip.size // chunk_size) * chunk_size
clip = clip[:clip_length]
chunks = clip.reshape((-1, chunk_size))
ret = []
source = gen_white_noise(chunk_size) if source_type == 'noise' else gen_pulse(chunk_size, source_freq)
for chunk, source in zip(chunks, source):
a = calc_ar_coeff_by_autocorrelation(chunk, p)
source = np.concatenate([source, np.zeros(source.size, dtype=np.float32)])
y = signal.lfilter(np.array([1]), a, source)
ret.append(y)
ret = np.vstack(ret)
ret[1:, :chunk_size] += ret[:-1, chunk_size:] # overlap add
return np.concatenate(ret[:, :chunk_size])
結果
パルスで駆動したデータは雑音が目立ちますね。やはり単純にパルスやノイズで駆動するだけでは綺麗な音声にはならない様です。 あとは、もう少しチャンク間の結合を工夫すれば良いのかもしれません。