Least-Squares Estimation of Transformation Parameters Between Two Point Patterns の読解

はじめに

拡大と回転と並進とによって実現する幾何学変換に相似変換があります．これは，画像間の位置合わせ等に用いられます． 具体的には，互いに対応する点\({x_{i}}\)と\(y_{i}\left(i = 1, 2, \dots n \right)\)が与えられた時，それらの間に存在する相似変換を推定するといったものです．

これを実現アルゴリズムにS.Umeyamaによって提案された手法があります．古典的な手法ではありますが，実用的なアルゴリズムであると思います．scikit-imageにおけるSimilalityTransformでも使用されています．

やったこと

• Least-Squares Estimation of Transformation Parameters Between Two Point Patternsによる提案手法を読む
• Pythonによる簡易的な実装

行列の性質復習

以下にこれから利用する行列の性質を示します．ここで，\(\mathbf A = \left(a_{i,j}\right)\)及び\(\mathbf B = \left(b_{i,j}\right)\)は行列を，\(\left<\cdot, \cdot\right>\)は行列の内積を表します．

\[ \begin{aligned} \mathrm {tr} \mathbf A &= \mathrm {tr} \mathbf A^{\mathrm T} \\ \mathrm {tr} \mathbf A \mathbf B \mathbf C &= \mathrm {tr} \mathbf B \mathbf C \mathbf A \\ \mathrm {tr} \mathbf A^{\mathrm T} \mathbf B &= \left<\mathbf A, \mathbf B \right> \\ &= \left\|\mathbf A \mathbf B \right\|^{2} \\ \frac{\partial}{\partial \mathbf A} \mathrm {tr} \left(\mathbf A \mathbf B\right) &= \mathbf B^{T} \\ \frac{\partial}{\partial \mathbf A} \mathrm {tr} \left(\mathbf A^{\mathrm T} \mathbf B\right) &= \mathbf B \\ \frac{\partial}{\partial \mathbf A} \mathrm {tr} \left(f\left(\mathbf A\right) g\left(\mathbf A\right)\right) &= \frac{\partial}{\partial \mathbf A_{1}} \mathrm {tr} \left(f\left(\mathbf A_{1}\right) g\left(\mathbf A\right)\right) + \frac{\partial}{\partial \mathbf A_{2}} \mathrm {tr} \left(f\left(\mathbf A\right) g\left(\mathbf A_{2}\right)\right) \\ \left<\mathbf A, \mathbf B \right> &= \mathrm {tr} \mathbf A^{\mathrm T} B \\ &= \sum_{i,j} a_{j,i}b_{i,j} \end{aligned} \]

相似変換について

上述したとおり，相似変換とは拡大と回転と並進とによって実現する幾何学的変換です．従って，変換元を\(\mathbf x\)，変換先を\(\mathbf x'\)，拡大率，回転行列，並進ベクトルをそれぞれ\(\left(c, \mathbf R, \mathbf t \right)\)とすると

\[ \begin{aligned} \mathbf x' &= c\mathbf R \mathbf x + \mathbf t \end{aligned} \]

と表されます．

ここで，特徴点\(\mathbf x_{i}\)と，その相似変換による変換\(\mathbf y_{i}\ \left(i = 1, 2, \dots , n \right)\)を観測した場合を考えます．この時，以下の\(e\left(c, \mathbf R, \mathbf t\right)\)を最小化することで，\(\mathbf x_{i}\)と\(\mathbf y_{i}\)から相似変換のパラメータ\(\left(c, \mathbf R, \mathbf t \right)\)を推定することができます．

\[ \begin{aligned} e^{2}\left(c, \mathbf R, \mathbf t\right) &= \frac{1}{n} \sum_{i=1}^{n} \left| \mathbf y_{i} - \left(c\mathbf R \mathbf x_{i} + \mathbf t\right)\right|^{2} \end{aligned} \]

回転行列の推定

相似変換に推定の先立ち，まずは以下の式を最小化する\(\mathbf R\)を推定することを考えます．ここで，\(\mathbf A\)及び\(\mathbf B\)は\(m \times n\)の行列を，\(\mathbf R\)は\(m \times m\)の行列を表します．

\[ \begin{alignedat}{4} \text{minimize} & \ \ \ \ \ & \left\| \mathbf A - \mathbf R \mathbf B\right\|^{2} & \\ \text{subject to} &\ &\left|\mathbf R \right| &= 1& \\ &\ & \mathbf R\mathbf R^{\mathrm T} &= \mathbf I \end{alignedat} \]

\(\mathbf R\)を適切に推定するためには，与えられた束縛条件の元で目的関数を最小化する必要があります．従って，ラグランジュの未定乗数法を用います．ここでは，ラグランジュ関数\(F\)は以下の様に表されます．なお，\(l_{i,j}\)及び\(g\)はラグランジュ乗数となります．

\[ \begin{aligned} F &= \left\|\mathbf A - \mathbf R \mathbf B \right\|^{2} + \sum_{i=1}^{m} \sum_{j=1}^{m} l_{i,j} \left(\mathbf R^{\mathrm T}\mathbf R - \mathbf I \right)_{i,j} + g\left(\left|\mathbf R \right| - 1 \right) \end{aligned} \]

上式において，\(\mathbf R^{\mathrm T}\mathbf R\)と\(\mathbf I\)は対象行列です．従って，それらの差である$ (R^{T}R - I )\(も対象行列となります．\) (R^{T}R - I )$が対象行列であるならば，対象な成分に対応するラグランジュ乗数も同様に等しくなります．すなわち，

\[ \begin{aligned} l_{i,j} &= l_{j,i} \end{aligned} \]

となります．従って，ラグランジュ関数の第2項は以下の様に表現することが可能です．

\[ \begin{aligned} \sum_{i=1}^{m} \sum_{j=1}^{m} l_{i,j} \left(\mathbf R^{\mathrm T}\mathbf R - \mathbf I \right)_{i,j}　&= \left< \left(l_{i,j}\right), \mathbf R^{\mathrm T}\mathbf R - \mathbf I \right>\\ &= \mathrm{tr} \left(\left(l_{j,i}\right) \left(\mathbf R^{\mathrm T}\mathbf R - \mathbf I \right)\right)\\ &= \mathrm{tr} \left(\left(l_{i,j}\right) \left(\mathbf R^{\mathrm T}\mathbf R - \mathbf I \right)\right)\\ \end{aligned} \]

ここで，

\[ \begin{aligned} \mathbf L &= \left(l_{i,j} \right) \end{aligned} \]

と置くと，

\[ \begin{aligned} \mathrm{tr} \left(\left(l_{i,j}\right) \left(\mathbf R^{\mathrm T}\mathbf R - \mathbf I \right)\right)　&= \mathrm{tr}\left( \mathbf L \left(\mathbf R^{\mathrm T}\mathbf R - \mathbf I \right)\right)\\ \end{aligned} \]

と表すことができます．従って，ラグランジュ関数\(F\)は以下の様に表現されます．

\[ \begin{aligned} F &= \left\|\mathbf A - \mathbf R \mathbf B \right\|^{2} + \mathrm{tr} \left(\mathbf L \left(\mathbf R^{\mathrm T}\mathbf R - \mathbf I \right) \right) + g\left(\left|\mathbf R \right| - 1 \right) \\ \end{aligned} \]

\(F\)を最小化する\(\mathbf R\)を求めるためには，以下の式を\(\mathbf R\)について解く必要があります．

\[ \begin{aligned} \frac{\partial F}{\partial \mathbf R} &= \frac{\partial}{\partial \mathbf R} \left\|\mathbf A - \mathbf R \mathbf B \right\|^{2} + \frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\mathbf L \left(\mathbf R^{\mathrm T}\mathbf R - \mathbf I \right) \right) +\frac{\partial}{\partial \mathbf R} g\left(\left|\mathbf R \right| - 1 \right) \\ &= 0 \end{aligned} \]

まずは，右辺第１項について考えます．

\[ \begin{aligned} \frac{\partial}{\partial \mathbf R} \left\|\mathbf A - \mathbf R \mathbf B \right\|^{2} &= \frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\left(\mathbf A - \mathbf R \mathbf B \right)^{\mathrm T}\left(\mathbf A - \mathbf R \mathbf B \right)\right) \\ &= \frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\mathbf A^{\mathrm T} \mathbf A - \mathbf A^{\mathrm T}\mathbf R \mathbf B - \mathbf B^{\mathrm T}\mathbf R^{\mathrm T} \mathbf A + \mathbf B^{\mathrm T}\mathbf R^{\mathrm T} \mathbf R \mathbf B\right) \\ &= \frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\mathbf A^{\mathrm T} \mathbf A\right) - \frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\mathbf A^{\mathrm T}\mathbf R \mathbf B\right) + \frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\mathbf B^{\mathrm T}\mathbf R^{\mathrm T} \mathbf A \right) +\frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\mathbf B^{\mathrm T}\mathbf R^{\mathrm T} \mathbf R \mathbf B\right) \\ &= - \frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\mathbf B \mathbf A^{\mathrm T}\mathbf R\right) - \frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\mathbf A\mathbf B^{\mathrm T}\mathbf R^{\mathrm T}\right) +\frac{\partial}{\partial \mathbf R_{1}} \mathrm{tr} \left(\mathbf B^{\mathrm T}\mathbf R_{1}^{\mathrm T} \mathbf R \mathbf B\right) +\frac{\partial}{\partial \mathbf R_{2}} \mathrm{tr} \left(\mathbf B^{\mathrm T}\mathbf R^{\mathrm T} \mathbf R_{2} \mathbf B\right) \\ \\ &= - \mathbf A \mathbf B^{\mathrm T} - \mathbf A\mathbf B^{\mathrm T} + \frac{\partial}{\partial \mathbf R_{1}} \mathrm{tr} \left(\mathbf R_{1}^{\mathrm T} \mathbf R \mathbf B\mathbf B^{\mathrm T}\right) +\frac{\partial}{\partial \mathbf R_{2}} \mathrm{tr} \left(\mathbf B\mathbf B^{\mathrm T}\mathbf R^{\mathrm T} \mathbf R_{2}\right) \\ \\ &= -2 \mathbf A \mathbf B^{\mathrm T} + \mathbf R \mathbf B \mathbf B^{\mathrm T} + \left(\mathbf B \mathbf B^{\mathrm T} \mathbf R^{\mathrm T} \right)^{\mathrm T} \\ &= -2 \mathbf A \mathbf B^{\mathrm T} + \mathbf R \mathbf B \mathbf B^{\mathrm T} + \mathbf R \mathbf B \mathbf B^{\mathrm T} \\ &= -2 \mathbf A \mathbf B^{\mathrm T} + 2\mathbf R \mathbf B \mathbf B^{\mathrm T} \end{aligned} \]

次に，右辺第２項について考えます．

\[ \begin{aligned} \frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\mathbf L \left(\mathbf R^{\mathrm T}\mathbf R - \mathbf I \right) \right) &= \frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\mathbf L \mathbf R^{\mathrm T}\mathbf R \right) - \frac{\partial}{\partial \mathbf R} \mathrm{tr} \left(\mathbf L\right) \\ &= \frac{\partial}{\partial \mathbf R_{1}} \mathrm {tr} \left(\mathbf L \mathbf R_{1}^{\mathrm T} \mathbf R \right) + \frac{\partial}{\partial \mathbf R_{2}} \mathrm {tr} \left(\mathbf L \mathbf R^{\mathrm T} \mathbf R_{2} \right) \\ &= \frac{\partial}{\partial \mathbf R_{1}} \mathrm {tr} \left(\mathbf R \mathbf L \mathbf R_{1}^{\mathrm T}\right) + \left(\mathbf L \mathbf R^{\mathrm T}\right)^{\mathrm T} \\ &= \mathbf R \mathbf L + \mathbf R \mathbf L^{\mathrm T}\\ &= \mathbf R \mathbf L + \mathbf R \mathbf L\\ &= 2\mathbf R \mathbf L \\ \end{aligned} \]

最後に，右辺第３項について考えます．

\[ \begin{aligned} \frac{\partial}{\partial \mathbf R} g\left(\left|\mathbf R \right| - 1 \right) &= g \frac{\partial}{\partial \mathbf R} \left|\mathbf R \right|\\ &= g \mathbf{R}\\ \end{aligned} \]

以上の結果より，

\[ \begin{aligned} \frac{\partial F}{\partial \mathbf R} &= -2 \mathbf A \mathbf B^{\mathrm T} + 2\mathbf R \mathbf B \mathbf B^{\mathrm T} + 2\mathbf R \mathbf L +g \mathbf{R} \\ &= 0\\ \end{aligned} \]

と表現することができます．上式を整理すると，

\[ \begin{aligned} 2\mathbf R \mathbf B \mathbf B^{\mathrm T} + 2\mathbf R \mathbf L +g \mathbf{R} &=2 \mathbf A \mathbf B^{\mathrm T} \\ \mathbf R\left(\mathbf B \mathbf B^{\mathrm T} + \mathbf L + \frac{1}{2}g \mathbf I \right) &= \mathbf A \mathbf B^{\mathrm T} \\ \end{aligned} \]

と表すことができます．ここで，

\[ \begin{aligned} \mathbf L' &= \mathbf B \mathbf B^{\mathrm T} + \mathbf L + \frac{1}{2}g \mathbf I \end{aligned} \]

と置きます．すると，

\[ \begin{aligned} \mathbf R\mathbf L' &= \mathbf A \mathbf B^{\mathrm T} \\ \mathbf L'^{\mathrm T}\mathbf R^{\mathrm T} &= \mathbf B \mathbf A^{\mathrm T} \\ \end{aligned} \]

となります．\(\mathbf B \mathbf B^{\mathrm T}\)，\(\mathbf L\)及び\(\mathbf I\)は全て対象行列です．従って，

\[ \begin{aligned} \mathbf L' &= \mathbf L'^{\mathrm T} \end{aligned} \]

という関係が成立します．従って，

\[ \begin{aligned} \mathbf L'\mathbf R^{\mathrm T} &= \mathbf B \mathbf A^{\mathrm T} \\ \end{aligned} \]

となります．ここで，両辺にそれぞれ自身の転置を掛けると，

\[ \begin{aligned} \mathbf L'\mathbf R^{\mathrm T} \left(\mathbf L'\mathbf R^{\mathrm T} \right)^{\mathrm T} &= \mathbf L'\mathbf R^{\mathrm T} \mathbf R \mathbf L'^{\mathrm T}\\ &= \mathbf L'\mathbf L'^{\mathrm T} \\ &= \mathbf L'^{2}\\ &= \mathbf B \mathbf A^{\mathrm T} \left(\mathbf B \mathbf A^{\mathrm T} \right)^{\mathrm T} \\ \end{aligned} \]

となります．また，\(\mathbf A\mathbf B^{\mathrm T}\)の特異値分解を以下の様に置きます．

\[ \begin{aligned} \mathbf A\mathbf B^{\mathrm T} &= \mathbf U \mathbf D \mathbf V^{\mathrm T} \end{aligned} \]

すると，

\[ \begin{aligned} \mathbf L'^{2} &= \left(\mathbf U \mathbf D \mathbf V^{\mathrm T} \right)^{\mathrm T} \mathbf U \mathbf D \mathbf V^{\mathrm T} \\ &= \mathbf V \mathbf D \mathbf U^{\mathrm T}\mathbf U \mathbf D \mathbf V^{\mathrm T} \\ &= \mathbf V \mathbf D^{2} \mathbf V^{\mathrm T} \\ \end{aligned} \]

であり，

\[ \begin{aligned} \mathbf L' &= \mathbf V \sqrt{\mathbf D^{2}} \mathbf V^{\mathrm T} \\ &= \mathbf V \begin{pmatrix} \ddots & & \\ & \sqrt{d_{i}^{2}}& \\ & & \ddots\\ \end{pmatrix} \mathbf V^{\mathrm T} \\ &= \mathbf V \begin{pmatrix} \ddots & & \\ & d_{i}s_{i}& \\ & & \ddots\\ \end{pmatrix} \mathbf V^{\mathrm T} \\ &= \mathbf V \mathbf D \mathbf S \mathbf V^{\mathrm T} \end{aligned} \]

と表すことができます．なお，\(\mathbf S = \mathop{\rm diag}s_{i}\ \left(s_{i} = \pm1\right)\)となります．

次に，上式の両辺に対して行列式を考えます．すると，

\[ \begin{aligned} \left| \mathbf L' \right| &= \left| \mathbf V \mathbf D \mathbf S \mathbf V^{\mathrm T} \right| \\ &= \left| \mathbf V \right| \cdot \left| \mathbf D\right| \cdot \left| \mathbf S\right| \cdot \left| \mathbf V^{\mathrm T} \right| \\ \end{aligned} \]

であり，\(\left|\mathbf V\right| = \left|\mathbf V^{\mathrm T}\right| = 1\)より，

\[ \begin{aligned} &= \left| \mathbf D\right| \cdot \left| \mathbf S\right| \\ \end{aligned} \]

また，

\[ \begin{aligned} \mathbf R\mathbf L' &= \mathbf A \mathbf B^{\mathrm T} \\ \mathbf R^{\mathrm T}\mathbf R\mathbf L' &= \mathbf R^{\mathrm T}\mathbf A \mathbf B^{\mathrm T} \\ \mathbf L' &= \mathbf R^{\mathrm T}\mathbf A \mathbf B^{\mathrm T} \\ \end{aligned} \]

であることから，

\[ \begin{aligned} \left| \mathbf L' \right| &= \left| \mathbf R^{\mathrm T} \right| \cdot \left| \mathbf A \mathbf B^{\mathrm T} \right| \\ &= \left| \mathbf A \mathbf B^{\mathrm T} \right| \\ \end{aligned} \]

となります．従って， \[ \begin{aligned} \left| \mathbf D\right| \cdot \left| \mathbf S\right| &= \left| \mathbf A \mathbf B^{\mathrm T} \right| \\ \end{aligned} \]

と表すことができます．また，特異値の性質より，\(d_{i} \geq 0\)であるため，

\[ \begin{aligned} \left| \mathbf D\right| &\geq 0 \\ \end{aligned} \]

となります．従って，

\[ \begin{aligned} \left| \mathbf S\right|&= \begin{cases} 1 & \ \ \ \text{if}\ \ \left| \mathbf A \mathbf B^{\mathrm T} \right| \geq 0 \\ -1 &\ \ \ \text{if}\ \ \left| \mathbf A \mathbf B^{\mathrm T} \right| \leq 0 \end{cases} \end{aligned} \]

となります．ここで，\(\left| \mathbf A - \mathbf R \mathbf B\right|^{2}\)の最小化について考えます．以上の結果より\(\left| \mathbf A - \mathbf R \mathbf B\right|^{2}\)は，

\[ \begin{aligned} \left\| \mathbf A - \mathbf R \mathbf B\right\|^{2} &= \mathrm{tr} \left(\left(\mathbf A - \mathbf R \mathbf B\right)^{\mathrm T} \left(\mathbf A - \mathbf R \mathbf B\right) \right) \\ &= \mathrm{tr}\left(\mathbf A^{\mathrm T}\mathbf A\right) - \mathrm{tr} \left(\mathbf A^{\mathrm T}\mathbf R \mathbf B\right) - \mathrm{tr} \left(\left(\mathbf R \mathbf B\right)^{\mathrm T}\mathbf A\right) + \mathrm{tr} \left(\left(\mathbf R \mathbf B\right)^{\mathrm T}\mathbf R \mathbf B\right)\\ &= \left\|\mathbf A\right\|^{2} - \mathrm{tr} \left(\left(\left(\mathbf R \mathbf B\right)^{\mathrm T}\mathbf A\right)^{\mathrm T}\right) - \mathrm{tr} \left(\left(\mathbf R \mathbf B\right)^{\mathrm T}\mathbf A\right) + \mathrm{tr} \left(\mathbf B^{\mathrm T} \mathbf R^{\mathrm T}\mathbf R \mathbf B\right)\\ &= \left\|\mathbf A\right\|^{2} - \mathrm{tr} \left(\left(\mathbf R \mathbf B\right)^{\mathrm T}\mathbf A\right) - \mathrm{tr} \left(\left(\mathbf R \mathbf B\right)^{\mathrm T}\mathbf A\right) + \mathrm{tr} \left(\mathbf B^{\mathrm T} \mathbf B\right)\\ &= \left\|\mathbf A\right\|^{2} + \left\|\mathbf B\right\|^{2} - 2 \mathrm{tr} \left(\left(\mathbf R \mathbf B\right)^{\mathrm T}\mathbf A\right)\\ &= \left\|\mathbf A\right\|^{2} + \left\|\mathbf B\right\|^{2} - 2 \mathrm{tr} \left(\mathbf B^{\mathrm T}\mathbf R^{\mathrm T} \mathbf A\right)\\ &= \left\|\mathbf A\right\|^{2} + \left\|\mathbf B\right\|^{2} - 2 \mathrm{tr} \left(\mathbf R^{\mathrm T} \mathbf A\mathbf B^{\mathrm T}\right)\\ &= \left\|\mathbf A\right\|^{2} + \left\|\mathbf B\right\|^{2} - 2 \mathrm{tr} \left(\mathbf L'\right)\\ &= \left\|\mathbf A\right\|^{2} + \left\|\mathbf B\right\|^{2} -2 \mathrm{tr} \left(\mathbf V\mathbf D\mathbf S\mathbf V^{\mathrm T}\right)\\ &= \left\|\mathbf A\right\|^{2} + \left\|\mathbf B\right\|^{2} -2 \mathrm{tr} \left(\mathbf D\mathbf S\mathbf V^{\mathrm T}\mathbf V\right)\\ &= \left\|\mathbf A\right\|^{2} + \left\|\mathbf B\right\|^{2} -2 \mathrm{tr} \left(\mathbf D\mathbf S\right)\\ &= \left\|\mathbf A\right\|^{2} + \left\|\mathbf B\right\|^{2} -2 \left(d_{1}s_{1} + d_{2}s_{2} + \cdots + d_{m}s_{m} \right)\\ \end{aligned} \]

と表すことができます．ここで，\(\mathbf A\)，\(\mathbf B\)，\(d_{i}\)が問題より与えられており，\(\left\|\mathbf A\right\|^{2} \ge 0\)，\(\left\|\mathbf B\right\|^{2} \ge 0\)となります．従って，\(\text{minimize}\ \left\| \mathbf A - \mathbf R \mathbf B\right\|^{2}\)は以下の様に書き換えることができます．

\[ \begin{alignedat}{4} \text{maximize} & \ \ \ \ \ & d_{1}s_{1} + d_{2}s_{2} + \cdots + d_{m}s_{m} & \\ \text{subject to} &\ & s_{1}s_{2} \cdots s_{m} &= \begin{cases} 1 & \ \ \ \text{if}\ \ \left| \mathbf A \mathbf B^{\mathrm T} \right| \geq 0 \\ -1 & \ \ \ \text{if}\ \ \left| \mathbf A \mathbf B^{\mathrm T} \right| \leq 0 \end{cases}& \\ &\ & \left| s_{i} \right| &= 1 \end{alignedat} \]

まず，\(\left| \mathbf A \mathbf B^{\mathrm T} \right| \geq 0\)の場合について考えます．この時，\(s_{i}=1\)で目的関数が最大化することは明らかです．次に，$ | A B^{T} | \(の場合について考えます．\)d_{1} d_{2} d_{m}\(であるため，\)s_{1} = s_{2} = = s_{m-1} = 1\(，\)s_{m} = -1$で目的関数が最大化します．

最後に，以上の結果を元に実際に\(\mathbf R\)を求めていきます．まず，\(\mathrm{rank}\left(\mathbf A \mathbf B^{\mathrm T}\right) = m\)である場合を考えます．この時，\(\mathbf L'\)は正則行列となります．よって，

\[ \begin{aligned} \mathbf L'^{-1} &= \left(\mathbf V \mathbf D \mathbf S \mathbf V^{\mathrm T}\right)^{-1} \\ &= \left( \mathbf V^{\mathrm T} \right)^{-1} \mathbf S^{-1} \mathbf D^{-1} \mathbf V^{-1} \\ &= \mathbf V \mathbf S \mathbf D^{-1} \mathbf V^{\mathrm T} \\ &= \mathbf V \mathbf D^{-1}\mathbf S \mathbf V^{\mathrm T} \end{aligned} \]

となります．従って，

\[ \begin{aligned} \mathbf R &= \mathbf A \mathbf B^{\mathrm T} \mathbf L'^{-1} \\ &= \mathbf U \mathbf D \mathbf V^{\mathrm T} \mathbf V \mathbf D^{-1} \mathbf S \mathbf V^{\mathrm T}\\ &= \mathbf U \mathbf S \mathbf V^{\mathrm T} \end{aligned} \]

となります．次に，\(\mathrm{rank}\left(\mathbf A \mathbf B^{\mathrm T}\right) = m-1\)である場合を考えます．

\[ \begin{aligned} \mathbf A \mathbf B^{\mathrm T} &=\mathbf U \mathbf D \mathbf V^{\mathrm T}\\ \mathbf L' &= \mathbf V \mathbf D \mathbf S \mathbf V^{\mathrm T} \\ \mathbf R\mathbf L' &= \mathbf A \mathbf B^{\mathrm T} \\ \end{aligned} \]

であるため， \[ \begin{aligned} \mathbf R\mathbf L' &= \mathbf A \mathbf B^{\mathrm T}\\ \mathbf R\left(\mathbf V \mathbf D \mathbf S \mathbf V^{\mathrm T} \right) &= \mathbf U \mathbf D \mathbf V^{\mathrm T}\\ \mathbf R\mathbf V \mathbf D \mathbf S \mathbf V^{\mathrm T} \mathbf V &= \mathbf U \mathbf D \mathbf V^{\mathrm T}\mathbf V\\ \mathbf R\mathbf V \mathbf D \mathbf S &= \mathbf U \mathbf D \\ \end{aligned} \]

ここで，\(\mathrm{rank}\left(\mathbf A \mathbf B^{\mathrm T}\right) = m-1\)であるため，\(d_{m} = 0\)となります．また，\(s_{1} = s_{2} = \cdots = s_{m} = 1\)であるため，

\[ \begin{aligned} \mathbf D\mathbf S &= \mathbf D\\ \end{aligned} \]

となります．よって，

\[ \begin{aligned} \mathbf R\mathbf V \mathbf D &= \mathbf U \mathbf D \\ \end{aligned} \]

ここで， \[ \begin{aligned} \mathbf Q &= \mathbf U^{\mathrm T} \mathbf R\mathbf V \\ \left| \mathbf Q \right| &= \left| \mathbf U^{\mathrm T} \mathbf R\mathbf V \right|\\ &= \left| \mathbf U^{\mathrm T}\right|\left| \mathbf R\right| \left|\mathbf V \right|\\ &= \left| \mathbf U\right|\left|\mathbf V \right| \end{aligned} \]

と置くと，

\[ \begin{aligned} \mathbf U^{\mathrm T} \mathbf R\mathbf V \mathbf D &=\mathbf U^{\mathrm T} \mathbf U \mathbf D \\ \mathbf Q\mathbf D &= \mathbf D \\ \end{aligned} \]

と表すことができます．さらに

\[ \begin{aligned} \mathbf Q &= \left(\mathbf q_{1} \mathbf q_{2} \cdots \mathbf q_{m} \right)\\ \mathbf e_{i} &= \left(e_{i,1}, e_{i,2}, \cdots, e_{i,m}\right)^{\mathrm T} \\ e_{i,j} &= \begin{cases} 0 & \ \ \ \text{otherwise} \\ 1 & \ \ \ \text{if}\ \ i=j \end{cases} \end{aligned} \]

と置くと，

\[ \begin{aligned} d_{i} \mathbf q_{i} &= d_{i}\mathbf e_{i} \\ \mathbf q_{i} &= \mathbf e_{i} \ \left( 1 \leq i \leq m - 1\right) \end{aligned} \]

となります．また，\(\mathbf U\), \(\mathbf R\), \(\mathbf V\)は全て直交行列です．従って\(\mathbf Q\)も同様に直交行列となります．そのため，\(\mathbf q_{m}\)は\(\mathbf q_{1} \cdots \mathbf q_{m-1}\)と直交します．従って，

\[ \begin{aligned} \mathbf q_{m} = \begin{cases} \mathbf e_{m} & \ \ \ \text{if}\ \ \left| \mathbf U\right|\left|\mathbf V \right| = 1\\ -\mathbf e_{m} & \ \ \ \text{if}\ \ \left| \mathbf U\right|\left|\mathbf V \right| = -1 \end{cases} \end{aligned} \]

となります．以上の結果より，

\[ \begin{aligned} \mathrm{svd} \left(\mathbf A\mathbf B^{\mathrm T}\right) &= \mathbf U \mathbf D \mathbf V^{\mathrm T}\\ \mathbf S &= \begin{cases} \mathbf I & \ \ \ \text{if}\ \ \left| \mathbf U\right|\left|\mathbf V \right| = 1\\ \mathrm{diag} \ \left(1, 1, \cdots, 1, -1\right) & \ \ \ \text{if}\ \ \left| \mathbf U\right|\left|\mathbf V \right| = -1 \end{cases}\\ \mathbf R &= \mathbf U \mathbf Q \mathbf V^{\mathrm T}\\ &= \mathbf U \mathbf S \mathbf V^{\mathrm T}\\ \end{aligned} \]

相似変換の推定

前述した通り，相似変換は以下の\(e^{2}\left(c, \mathbf R, \mathbf t\right)\)を最小化する\(c, \mathbf R, \mathbf t\)を求めることによって与えられます．

\[ \begin{aligned} e^{2}\left(c, \mathbf R, \mathbf t\right) &= \frac{1}{n} \sum_{i=1}^{n} \left| \mathbf y_{i} - \left(c\mathbf R \mathbf x_{i} + \mathbf t\right)\right|^{2} \end{aligned} \]

ここで，\(\mathbf X= \left(\mathbf x_{1}, \mathbf x_{2}, \cdots, \mathbf x_{n}\right)\)，\(\mathbf Y= \left(\mathbf y_{1}, \mathbf y_{2}, \cdots, \mathbf y_{n}\right)\)，\(\mathbf h = \left(1, 1, \cdots, 1\right)^{\mathrm T}\)と置くと，

\[ \begin{aligned} e^{2}\left(c, \mathbf R, \mathbf t\right) &= \frac{1}{n} \left\| \mathbf Y - c \mathbf R \mathbf X -\mathbf t \mathbf h^{\mathrm T} \right\|^{\mathrm 2} \end{aligned} \]

と表現することができます．また，

\[ \begin{aligned} \mathbf K &= \mathbf I - \frac{1}{n} \mathbf h \mathbf h^{\mathrm T} \\ \mathbf K &= \mathbf K^{\mathrm T}\\ \mathbf K \mathbf K^{\mathrm T} &= \mathbf K \end{aligned} \]

とすると，

\[ \begin{aligned} \mathbf X\mathbf K &= \mathbf X\left(\mathbf I - \frac{1}{n} \mathbf h \mathbf h^{\mathrm T} \right)\\ &= \mathbf X - \frac{1}{n}\mathbf X\mathbf h \mathbf h^{\mathrm T}\\ \mathbf X &= \mathbf X\mathbf K + \frac{1}{n}\mathbf X \mathbf h \mathbf h^{\mathrm T} \end{aligned} \]

であり，同様に，

\[ \begin{aligned} \mathbf Y &= \mathbf Y\mathbf K + \frac{1}{n}\mathbf Y \mathbf h \mathbf h^{\mathrm T} \end{aligned} \]

これらを用いて，\(e^{2}\left(c, \mathbf R, \mathbf t\right)\)を表すと，

\[ \begin{aligned} e^{2}\left(c, \mathbf R, \mathbf t\right) &= \frac{1}{n} \left\| \mathbf Y\mathbf K + \frac{1}{n}\mathbf Y \mathbf h \mathbf h^{\mathrm T} - c \mathbf R \left(\mathbf X\mathbf K + \frac{1}{n}\mathbf X \mathbf h \mathbf h^{\mathrm T}\right) -\mathbf t \mathbf h^{\mathrm T} \right\|^{\mathrm 2}\\ &= \frac{1}{n} \left\| \mathbf Y\mathbf K + \frac{1}{n}\mathbf Y \mathbf h \mathbf h^{\mathrm T} - c \mathbf R \mathbf X\mathbf K -\frac{c}{n}\mathbf R\mathbf X \mathbf h \mathbf h^{\mathrm T} -\mathbf t \mathbf h^{\mathrm T} \right\|^{\mathrm 2}\\ &= \frac{1}{n} \left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K + \left(\frac{1}{n}\mathbf Y \mathbf h -\frac{c}{n}\mathbf R\mathbf X \mathbf h -\mathbf t\right) \mathbf h^{\mathrm T} \right\|^{\mathrm 2}\\ &= \frac{1}{n} \left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K - \mathbf t' \mathbf h^{\mathrm T} \right\|^{\mathrm 2}\\ &= \frac{1}{n} \mathrm{tr}\left(\left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K - \mathbf t' \mathbf h^{\mathrm T} \right)^{\mathrm T}\left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K - \mathbf t' \mathbf h^{\mathrm T} \right) \right)\\ &= \frac{1}{n} \mathrm{tr}\left(\left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right)^{\mathrm T}\left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right) - \left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right)^{\mathrm T}\left(\mathbf t' \mathbf h^{\mathrm T} \right) -\left(\mathbf t' \mathbf h^{\mathrm T}\right)^{\mathrm T}\left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right) +\left(\mathbf t' \mathbf h^{\mathrm T}\right)^{\mathrm T}\left(\mathbf t' \mathbf h^{\mathrm T} \right) \right)\\ &= \frac{1}{n}\left\{ \mathrm{tr}\left( \left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right)^{\mathrm T}\left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right) \right) -\mathrm{tr}\left( \left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right)^{\mathrm T}\left(\mathbf t' \mathbf h^{\mathrm T} \right) \right) -\mathrm{tr}\left( \left(\mathbf t' \mathbf h^{\mathrm T}\right)^{\mathrm T}\left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right)\right)+\mathrm{tr}\left( \left(\mathbf t' \mathbf h^{\mathrm T}\right)^{\mathrm T}\left(\mathbf t' \mathbf h^{\mathrm T} \right) \right) \right\}\\ &= \frac{1}{n}\left\{ \left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right\|^{2} + \left\|\mathbf t' \mathbf h^{\mathrm T} \right\|^{2} -\mathrm{tr}\left( \left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right)^{\mathrm T}\left(\mathbf t' \mathbf h^{\mathrm T} \right) \right) -\mathrm{tr}\left(\left( \left(\mathbf t' \mathbf h^{\mathrm T}\right)^{\mathrm T}\left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right) \right)^{\mathrm T}\right) \right\}\\ &= \frac{1}{n}\left\{ \left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right\|^{2} + \left\|\mathbf t' \mathbf h^{\mathrm T} \right\|^{2} -\mathrm{tr}\left( \left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right)^{\mathrm T}\left(\mathbf t' \mathbf h^{\mathrm T} \right) \right) -\mathrm{tr}\left( \left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right)^{\mathrm T} \left(\mathbf t' \mathbf h^{\mathrm T}\right) \right) \right\}\\ &= \frac{1}{n}\left\{ \left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right\|^{2} + \left\|\mathbf t' \mathbf h^{\mathrm T} \right\|^{2} -2\mathrm{tr}\left( \left(\mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right)^{\mathrm T}\left(\mathbf t' \mathbf h^{\mathrm T} \right) \right) \right\}\\ &= \frac{1}{n}\left\{ \left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right\|^{2} + \left\|\mathbf t' \mathbf h^{\mathrm T} \right\|^{2} -2\mathrm{tr}\left( \left(\mathbf K^{\mathrm T}\mathbf Y^{\mathrm T} - c \mathbf K^{\mathrm T} \mathbf X^{\mathrm T}\mathbf R^{\mathrm T}\right)\left(\mathbf t' \mathbf h^{\mathrm T} \right) \right) \right\}\\ &= \frac{1}{n}\left\{ \left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right\|^{2} + \left\|\mathbf t' \mathbf h^{\mathrm T} \right\|^{2} -2\mathrm{tr}\left(\mathbf K^{\mathrm T} \left(\mathbf Y^{\mathrm T} - c \mathbf X^{\mathrm T}\mathbf R^{\mathrm T}\right)\left(\mathbf t' \mathbf h^{\mathrm T} \right) \right) \right\}\\ &= \frac{1}{n}\left\{ \left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right\|^{2} + \left\|\mathbf t' \mathbf h^{\mathrm T} \right\|^{2} -2\mathrm{tr}\left(\mathbf K \left(\mathbf Y^{\mathrm T} - c \mathbf X^{\mathrm T}\mathbf R^{\mathrm T}\right)\left(\mathbf t' \mathbf h^{\mathrm T} \right) \right) \right\}\\ \end{aligned} \]

なお，

\[ \begin{aligned} \mathbf t' &= -\frac{1}{n}\mathbf Y \mathbf h +\frac{c}{n}\mathbf R\mathbf X \mathbf h +\mathbf t \end{aligned} \]

と置いています．ここで，右辺第３項について考えます． \[ \begin{aligned} \mathrm{tr}\left(\mathbf K \left(\mathbf Y^{\mathrm T} - c \mathbf X^{\mathrm T}\mathbf R^{\mathrm T}\right)\mathbf t' \mathbf h^{\mathrm T} \right) &=\mathrm{tr}\left(\mathbf h^{\mathrm T} \mathbf K \left(\mathbf Y^{\mathrm T} - c \mathbf X^{\mathrm T}\mathbf R^{\mathrm T}\right)\mathbf t' \right) \\ &= \mathrm{tr}\left(\mathbf h^{\mathrm T} \left( \mathbf I - \frac{1}{n} \mathbf h \mathbf h^{\mathrm T} \right) \left(\mathbf Y^{\mathrm T} - c \mathbf X^{\mathrm T}\mathbf R^{\mathrm T}\right)\mathbf t' \right) \\ &= \mathrm{tr}\left( \left( \mathbf h^{\mathrm T} - \frac{1}{n} \mathbf h^{\mathrm T}\mathbf h \mathbf h^{\mathrm T} \right) \left(\mathbf Y^{\mathrm T} - c \mathbf X^{\mathrm T}\mathbf R^{\mathrm T}\right)\mathbf t' \right) \\ &= \mathrm{tr}\left( \left( \mathbf h^{\mathrm T} - \mathbf h^{\mathrm T} \right) \left(\mathbf Y^{\mathrm T} - c \mathbf X^{\mathrm T}\mathbf R^{\mathrm T}\right)\mathbf t' \right) \\ &= 0 \end{aligned} \]

次に右辺第２項について考えます． \[ \begin{aligned} \left\|\mathbf t'\mathbf h^{\mathrm T} \right\|^{2}&= n\left\| \mathbf t'\right\|^{2} \end{aligned} \]

以上の結果より，

\[ \begin{aligned} e^{2}\left(c, \mathbf R, \mathbf t\right) &= \frac{1}{n} \left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right\|^{2} + \left\| \mathbf t'\right\|^{2} \end{aligned} \]

と表されます．\(e^{2}\left(c, \mathbf R, \mathbf t\right)\)を最小化するために，\(\mathbf t'=0\)と置くと，

\[ \begin{aligned} \mathbf t' &= -\frac{1}{n}\mathbf Y \mathbf h +\frac{c}{n}\mathbf R\mathbf X \mathbf h +\mathbf t\\ &= 0\\ \end{aligned} \]

従って，

\[ \begin{aligned} \mathbf t &= \frac{1}{n}\mathbf Y \mathbf h - \frac{c}{n}\mathbf R\mathbf X \mathbf h \end{aligned} \]

ここで， \[ \begin{aligned} \mathbf{\mu_{y}} &= \frac{1}{n}\mathbf Y \mathbf h\\ \mathbf{\mu_{x}} &= \frac{1}{n}\mathbf X \mathbf h \end{aligned} \]

と置くと， \[ \begin{aligned} \mathbf t &= \mathbf{\mu_{y}} - c\mathbf R\mathbf{\mu_{x}} \end{aligned} \]

並進成分が求まったので，再度評価関数\(e^{2}\)を書き下すと，

\[ \begin{aligned} e^{2}\left(c, \mathbf R, \mathbf t = \mathbf{\mu_{y}} - c\mathbf R\mathbf{\mu_{x}}\right) &= \frac{1}{n} \left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right\|^{2} \end{aligned} \]

ここで，\(\frac{1}{n}\mathbf Y \mathbf K \mathbf X^{\mathrm T}\)の特異値分解を以下の様に置きます． \[ \begin{aligned} \frac{1}{n}\mathbf Y \mathbf K \mathbf X^{\mathrm T} &= \mathbf U \mathbf D \mathbf V^{\mathrm T} \end{aligned} \]

すると，

\[ \begin{aligned} \left(\mathbf Y \mathbf K\right)\left(c\mathbf X \mathbf K\right)^{\mathrm T} &= c\mathbf Y \mathbf K \mathbf K^{\mathrm T}\mathbf X^{\mathrm T}\\ &= c \mathbf Y \mathbf K\mathbf X^{\mathrm T}\\ &= cn\mathbf U \mathbf D\mathbf V^{\mathrm T}\\ \end{aligned} \]

また，回転行列の推定の結果より， \[ \begin{aligned} \frac{1}{n}\left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right\|^{2} &= \frac{1}{n} \left\{ \left\|\mathbf Y \mathbf K\right\|^{2} + c^{2}\left\|\mathbf X \mathbf K\right\|^{2} - 2\mathrm{tr} \left(cn\mathbf U \mathbf D\mathbf V^{\mathrm T}\right) \right\} \end{aligned} \]

上式を\(c\)について最小化すると，

\[ \begin{aligned} \frac{\partial}{\partial c} \frac{1}{n}\left\| \mathbf Y\mathbf K - c \mathbf R \mathbf X\mathbf K\right\|^{2}&= \frac{1}{n} \left\{2 c\left\|\mathbf X \mathbf K\right\|^{2} - 2n\mathrm{tr} \left(\mathbf U \mathbf D\mathbf V^{\mathrm T}\right) \right\}\\ &= 0\\ c &= \frac{\mathrm{tr} \left(\mathbf D\mathbf S\right)}{\frac{1}{n}\left\|\mathbf X\mathbf K\right\|^{2}} \end{aligned} \]

ここで，

\[ \begin{aligned} \sigma_{x}^{2}&= \frac{1}{n}\left\|\mathbf X\mathbf K\right\|^{2} \end{aligned} \]

とおくと，

\[ \begin{aligned} c &= \frac{\mathrm{tr} \left(\mathbf D\mathbf S\right)}{\sigma_{x}^{2}} \end{aligned} \]

また，回転行列\(\mathbf R\)についても同様に

\[ \begin{aligned} \mathbf R &= \mathbf U \mathbf S \mathbf V^{\mathrm T}\\ \mathbf S &= \begin{cases} \mathbf I & \ \ \ \text{if}\ \ \left| \mathbf U\right|\left|\mathbf V \right| = 1\\ \mathrm{diag} \ \left(1, 1, \cdots, 1, -1\right) & \ \ \ \text{if}\ \ \left| \mathbf U\right|\left|\mathbf V \right| = -1 \end{cases}\\ \end{aligned} \]

以上の結果をまとめると， \[ \begin{aligned} c &= \frac{\mathrm{tr} \left(\mathbf D\mathbf S\right)}{\sigma_{x}^{2}}\\ \mathbf R &= \mathbf U \mathbf S \mathbf V^{\mathrm T}\\ \mathbf S &= \begin{cases} \mathbf I & \ \ \ \text{if}\ \ \left| \mathbf U\right|\left|\mathbf V \right| = 1\\ \mathrm{diag} \ \left(1, 1, \cdots, 1, -1\right) & \ \ \ \text{if}\ \ \left| \mathbf U\right|\left|\mathbf V \right| = -1 \end{cases}\\ \mathbf t &= \mathbf{\mu_{y}} - c\mathbf R\mathbf{\mu_{x}}\\ \end{aligned} \]

Pythonによる実装

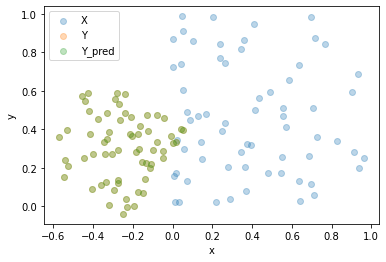
上述の方法をPythonで実装しました．青色の点が\(\mathbf X\)を，橙色の点が\(\mathbf Y\)を，緑色の点が\(c\mathbf R\mathbf X\)をそれぞれ表しています．橙色の点ど緑色の点が重なっていることから，パラメータの推定が適切に行われていることを確認できます．

import numpy as np
from random import random
import math
import matplotlib.pyplot as plt

n = 64
c = random() + 0.5
theta = math.pi * random()
cs, ss = math.cos(theta), math.sin(theta)
R = np.array([[cs, -ss], [ss, cs]])
t = np.random.rand(2, 1)

noise = 0.0 * np.random.rand(2, n)
X = np.random.rand(2, n)
Y = c * R @ X + t + noise
h = np.ones((n, 1))
K = np.eye(n) - 1 / n * h @ h.T

U, D, V = np.linalg.svd(Y @ K @ X.T / n) 
S = np.diag([1,np.linalg.det(U) * np.linalg.det(V) ])
R_pred = U @ S @ V.T
c_pred = n * np.trace(np.diag(D) @ S) / np.trace(X @ K @ X.T)
t_pred = ((Y @ h) - c_pred * R_pred @ X @ h) / n
Y_pred = c_pred * R_pred @ X + t_pred

ax = plt.gca()
ax.set_xlabel("x")
ax.set_ylabel("y")
plt.scatter(x = X[0,:], y =X[1,:], label="X", color="tab:blue", alpha=0.3)
plt.scatter(x = Y[0,:], y =Y[1,:], label="Y", color="tab:orange", alpha=0.3)
plt.scatter(x = Y_pred[0,:], y =Y_pred[1,:], label="Y_pred", color="tab:green", alpha=0.3)
ax.legend()
plt.show()

参考

[1]

Petersen, K.B. et al. 2008. The matrix cookbook. Technical University of Denmark. 7, 15 (2008), 510.

[2]

Umeyama, S. 1991. Least-squares estimation of transformation parameters between two point patterns. IEEE Transactions on Pattern Analysis & Machine Intelligence. 13, 04 (1991), 376–380.